개요

문제 이름: 약수의 합 (12928)
문제 링크: https://school.programmers.co.kr/learn/courses/30/lessons/12928
플랫폼: 프로그래머스
알고리즘 분류: 일반
소요 시간: 20분
문제 전문
설명

제한사항

입출력
문제 풀이
해설
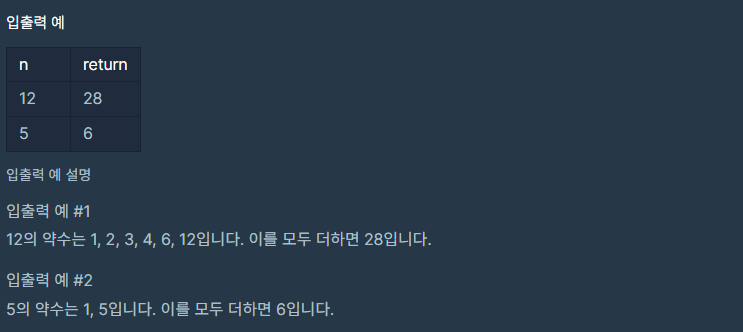
이 문제는 주어진 정수 n의 모든 약수를 찾아 그 합을 구하는 문제입니다. 약수란 어떤 수를 나누어 떨어지게 하는 수를 말합니다. 예를 들어, 12의 약수는 1, 2, 3, 4, 6, 12입니다.
이 문제를 해결하기 위한 기본적인 접근 방식은 1부터 n까지의 모든 수를 순회하면서 n을 나누어 떨어지게 하는 수를 찾아 더하는 것입니다. 하지만 이 방법은 n이 커질수록 비효율적일 수 있습니다.
더 효율적인 방법은 n의 제곱근까지만 순회하는 것입니다. 이는 약수의 특성을 이용한 것으로, n의 약수 중 제곱근보다 작은 수를 찾으면 그에 대응하는 큰 약수도 동시에 찾을 수 있기 때문입니다.
시도
1차 시도 (성공)
function solution(n) {
let sum = 0; // 약수의 합을 저장할 변수
// 1부터 n까지 모든 수를 확인
for (let i = 1; i <= n; i++) {
// 만약 n이 i로 나누어 떨어진다면 (나머지가 0이면)
if (n % i === 0) {
sum += i; // i는 n의 약수이므로 sum에 더함
}
}
return sum; // 모든 약수의 합을 반환
}이 코드는 가장 직관적인 방법으로 문제를 해결합니다. 1부터 n까지 모든 수를 순회하며, 각 수가 n의 약수인지 확인합니다. 약수라면 sum에 더합니다.
- let sum = 0: 약수의 합을 저장할 변수를 초기화합니다.
- for (let i = 1; i <= n; i++): 1부터 n까지 모든 수를 순회합니다.
- if (n % i === 0): n을 i로 나눈 나머지가 0인지 확인합니다. 0이라면 i는 n의 약수입니다.
- sum += i: i가 n의 약수일 경우, sum에 i를 더합니다.
시간복잡도: O(n), n이 커질수록 실행 시간이 선형적으로 증가합니다.
공간복잡도: O(n), n의 크기에 관계없이 일정한 메모리만을 사용합니다.
2차 시도 (성공)
function solution(n) {
let sum = 0;
// n의 제곱근까지만 확인하면 됨
for (let i = 1; i <= Math.sqrt(n); i++) {
if (n % i === 0) {
sum += i; // i는 약수
if (i !== n / i) {
// i와 n/i가 다르면 (예: 12의 경우 3과 4)
sum += n / i; // n/i도 약수
}
}
}
return sum;
}이 코드는 1차 시도보다 더 효율적인 방법을 사용합니다. n의 제곱근까지만 순회하면서 약수를 찾고, 찾은 약수에 대응하는 큰 약수도 동시에 처리합니다.
- Math.sqrt(n): JavaScript의 내장 함수로, n의 제곱근을 반환합니다.
- for (let i = 1; i <= Math.sqrt(n); i++): n의 제곱근까지만 순회합니다.
- if (n % i === 0): i가 n의 약수인지 확인합니다.
- sum += i: i가 약수라면 sum에 더합니다.
- if (i !== n / i): i와 n/i가 다른 경우 (예: 12의 약수 3과 4), n/i도 약수이므로 sum에 더합니다.
시간복잡도: O(√n), n이 커질수록 실행 시간이 제곱근에 비례하여 증가합니다.
공간복잡도: O(n).
'💻 종합 개발 주제 > ⌨️ 코딩 테스트' 카테고리의 다른 글
| [프로그래머스] JavaScript Lv2 - 예상 대진표(12985) (1) | 2024.07.31 |
|---|---|
| [프로그래머스] JavaScript Lv2 - 이진 변환 반복하기(70129) (1) | 2024.07.18 |
| [프로그래머스] JavaScript Lv2 - 최댓값과 최솟값(12939) (0) | 2024.07.11 |
| [프로그래머스] JavaScript Lv3 - 이중우선순위큐(42628) (1) | 2024.07.04 |
| [프로그래머스] JavaScript Lv2 - 게임 맵 최단거리(1844) (0) | 2024.06.26 |
